Trigonometry

Trigonometry

Trigonometric Ratios

• There are 3 (important) trigonometric ratios you need to learn: sine, cosine, and tangent
• These three ratios are based on the angles and side lengths of a right angle triangle

• If you have any 2 side lengths, you can calculate the values of all other angles and sides using these ratios
• However, THIS ONLY WORKS FOR RIGHT ANGLED TRIANGLES!!!

The ratios are as follows:

• $sin(angle)=\frac{opposite}{hypotenuse}\newcommand{deg}{^{\circ}}$

• $cos(angle)=\frac{adjacent}{hypotenuse}$

• $tan(angle)=\frac{opposite}{adjacent}$

To remember the ratios, a common mnemonic (memory device) is SOH CAH TOA:

Solving Problems using Trigonometric Ratios

1. Draw the triangle, labelling the angles and sides.

2. Use SOH CAH TOA to decide which formula to use.

3. Rearrange the formula to get the correct subject (whatever the question wants you to find).

4. Substitute and solve.

Example Question

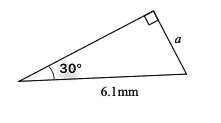
A right angled triangle has hypotenuse=$6.1mm$ and an angle of $30^\circ$. Find the length of the opposite side.

1. Diagram and labelling

2. SOH CAH TOA

Since we have an angle and the hypotenuse, and we need to find the opposite, sin is the formula to go with.

3. Rearrange

$\begin{eqnarray}sin(θ)=\frac{O}{H} \\ O=H\times\sin(θ)\end{eqnarray}\newcommand{dms}{\text{ }\enclose{roundedbox}{\text{ }\deg\text{’ ’’ }}\text{ }}$

4. Solve

$\begin{eqnarray}a=6.1\times\sin(30^{\circ}) \\ =3.05mm \end{eqnarray}\newcommand{orange}{\color{orange}}\newcommand{default}{\color{default}}$

Degrees, Minutes and Seconds

• Because trigonometry likes to be special, you typically don’t use decimal places when working with angles.
• Instead, a degree can be divided into minutes and seconds:
  • One degree = 60 minutes
  • 1 minute = 60 seconds
• When working with degrees, minutes, and seconds on a calculator, use the DMS button:

• For example, 82 degrees, 15 minutes, 25 seconds would be represented as $82\deg15'25’’,$ and typed as $82\dms15\dms25\dms$ into your calculator.

Angles of Elevation and Depression

• The angle of elevation is the angle measured upwards from the horizontal.
• The angle of depression is the angle measured downwards from the horizontal.

• Note that the angle of elevation and depression are equal, as they form alternate angles over parallel lines (Z shape).$\newcommand{true}{\deg \text{T}}$

Compass and True Bearings

• Compass bearings are directions given by stating the angle either side of north or south, such as $S60\deg E$
• True bearings are directions measured clockwise from north, terminated with the letter $\text{T}$, e.g. $120\true$

Obtuse Angle Trigonometry

• For angles below 90 degrees, sine, cosine, and tan are all positive. For angles greater than 180, however, they are not.
• For obtuse angles $\left(90\deg\ltθ\lt180\deg\right)$, only sine produces a positive result. Both cos and tan are negative.
  • For example, while $\sin{(120\deg)}=\mathbf{+}\frac{\sqrt{3}}{2},$ $\cos{(120\deg)}=-\frac{1}{2},$ and $\tan{(120\deg)}=-\sqrt{3}.$

Area Of A Triangle

• The area of a right-angled triangle can be calculated using $A=\frac{1}{2}bh.$

• However, this formula doesn’t work as easily for non-right triangles, as the triangle has to be split to find the perpendicular height and it’s just messy and unpleasant.

• Fortunately, as long as we know the length of 2 sides and the angle between them, we can use trig ratios to calculate the area of a triangle using known values: $$Area=\frac{1}{2}ab\times\sin\left(C\right)$$

• This formula can also be used for right-triangles too, and is on your reference sheet.

Sine Rule

• The sine rule relates the sides and angles in a triangle, and is used in a non-right-angled triangle given information about two sides and two angles:

$$\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$$

• Note that this can be flipped upside down too:

$$\frac{\sin(A)}{a}=\frac{\sin(B)}{b}=\frac{\sin(C)}{c}$$

• Usually, the top version is used to find a side, while the bottom version is used to find an angle, for example:
  • $\frac{a}{\sin(A)}\times\sin(B)=b$ can be used if you know angle B, angle A, and side A, and need to find side b.
  • $\frac{sin(A)}{a}\times b=\sin(B)$ can be used if you know, angle A, side A, and side b, and need to find angle B.

• Sine rule is used in a non-right-angled triangle given:
  • Two sides and an angle opposite one of the given sides, or
  • Two angles and one side

Cosine Rule

Cosine Rule is used in a non-right-angled triangle given information about three sides and one angle.

• To find the third side, given 2 sides and the included angle:

$$c^{2}=a^{2}+b^{2}-\left(2ab\times\cos\left(C\right)\right)$$

• To find the angle, given all three sides, you can rearrange the above formula:

$$cos(C)=\frac{a^2+b^2-c^2}{2ab}$$

Sine rule and Cosine rule are both on your reference sheet.