Table of Contents
What is a Network?
- A network is a visualisation of objects and how they are connected
- Networks have 3 key features:
- The Network is the entire visualisation
- The vertices (singular: vertex) are the objects in the network, represented as points/dots
- The Edges are the lines connecting the vertices
What properties can network features have?
- Vertices have a property known as its “degree”, which is the number of other unique vertices it is connected to
- Edges have two properties: weight (how strong the connection is) and direction (if a connection is one-way or two-way)
- Edges with direction have an arrow pointing in the direction they travel
- Loops are a special type of edge:
- A loop starts and ends at the same vertex
- It counts as 1 edge, but adds two to the degree of the vertex
How are Vertices represented?
- Vertices can be represented by listing them all in braces:
$\color{orange}{V= \{ A,B,C,D,E,F \} }$
How are Edges represented?
- Edges are represented by writing the start and end points in brackets
- For example, an edge between $A$ and $B$ would be represented as $(A,B)$
- A loop is represented the same as an edge, but with the vertex in both places
- For example, a loop around $X$ would be represented as $(X,X)$
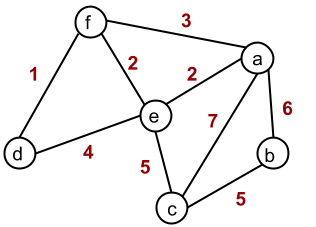
- In a Network diagram, the weight of an edge is written next to it as a label
The vertices are A, B, C, D, E, and F, and the weights of the edges are the numbers in red.
How are networks navigated?
- A walk is a connect set of edges from one vertex to another
- An example of a walk is a GPS guided drive, in which each street is an edge, and your start and end point are the vertices
- Usually, your aim is to find the shortest possible walk between any two vertices, or to find a path which includes every edge/vertex
What types of walk are there?
- A trail is a walk in which no edge is traversed more than once (i.e. no repeated edges)
- A path is a walk with no repeated vertices or edges
- A circuit is a walk with no repeated edges which starts at the same vertex it ends on
- A cycle is a walk with no repeated vertices which starts at the same vertex it ends on
This is “neatly” summarised by this flowchart:
How are Networks Drawn?
- Mark out every vertex IN PENCIL
- Connect any connected vertices with edges IN PENCIL
- Label each vertex
- Label the weight and direction of each edge
What is an isomorphic network?
- An isomorphic network is a network in which every edge has the same weight, and every vertex has the same degree
What are Eulerian Trails?
- Eulerian trails are trails which use every edge of a network exactly once
- By definition, they must start and end at different vertices
- Eulerian trails will always exist if there are exactly two vertices with an odd degree
- These two vertices must be the start and end of the trail
What are Eulerian Circuits?
- Eulerian circuits are a subset of eulerian trails
- They are identical to Eulerian trails in every way, except that they start and end at the same point (because they are circuits)
- Eulerian circuits will always exist if every vertex is of even degree
What is a Tree?
- A tree is a connected graph which has no cycles or loops
- In a tree, the number of edges is always 1 less than the number of vertices
What is a Spanning Tree?
- Within a network, there will always be a tree which can be created
- A tree which connects all of the vertices in a network is known as a spanning tree
- Minimum spanning trees are spanning trees which have the lowest possible total weight
- The sum of the weights of each edge should be as low as possible, while still connecting every vertex
What is Prim’s Algorithm?
- Prim’s algorithm is a set of rules to determine a minimum spanning tree of a graph:
- Choose any vertex (vertex 1)
- Follow the edge with the lowest weight to the next vertex (vertex 2)
- Follow the edge of vertex 2 with the lowest weight, excluding the edge connecting to vertex 1
- Repeat step 3, ignoring edges which will result in doubling up on a vertex, until all vertices are connected
What is a Connector Problem?
- Connector problems use minimum spanning trees to find the lowest cost method to link multiple objects to a network
- They usually take the form of “Which path will be the lowest cost, while reaching every vertex in the network?”
How can the Shortest Path Between Vertices be Calculated?
- The shortest path is the path between two vertices with the lowest total edge weight
- Following Prim’s algorithm between the two vertices is the most efficient way to do this
Found this post useful? Support us on Patreon.