Physics Module 1: Kinematics

Motion

• Motion is a fundamental observable phenomenon.
• The study of Kinematics involves describing, measuring, and analysing motion without considering the forces and masses involved.

Scalars and Vectors

• Scalars are physical quantities that can be described as a magnitude, with a unit (for example, 60km/h)
  • Examples of Scalars include time, distance, volume, and speed
  • Scalars are represented by a simple italic symbol, such as t for time or d for distance
• Vectors are physical quantities that can be described as a magnitude, a unit and a direction (for example, 20m West)
  • Examples of Vectors include position, displacement, velocity, acceleration, and force
  • Vectors are represented using VECTOR NOTATION.
    • The most common type of vector notation uses an arrow above the symbol, for example \(\vec{v}\) for Velocity

Adding and Subtracting Vectors Using Algebra (One Dimension)

• When adding or subtracting vectors using algebra, a sign convention must be established to represent the direction
  • For example, positive for forwards and negative for backwards
  • When using a sign convention it is CRUCIAL to provide a key explaining the convention used.
  • Using a sign convention allows you to enter the directions and magnitudes into your calculator. The sign of the final magnitude gives the direction of the total vector.

Steps for Adding:

1. Apply the sign convention to change each of the directions to signs
2. Add their magnitudes and their signs together
3. Refer to the sign convention to determine to direction of thr resultant vector
4. State the resultant vector

• Example:
  • A student walks 25m forward, then 16m backward, then 44m forward, then 12m backward. Determine the total displacement.
  1. Forward is positive
  • 25m forward = 25m
  • 16m backward = -16m
  • 44m forward = 44m
  • 12m backward = -12m
  2. \(25-16+44-12 = +41\)
  3. Positive is forward
  4. Therefore, the total displacement is 41m forward.

Steps for Subtracting

1. Apply the sign convention to change each of the directions to signs
2. Reverse the direction of the initial vector by reversing the sign
3. Do vector addition with the results

• Example:
  • An aeroplane changes course from 255m/s West to 160m/s East. Determine the change in velocity.
  1. West is negative
  • 225m/s West = -255m/s \(\vec{v}_1\)
  • 160m/s East = 160m/s \(\vec{v}_2\)
  2. Reverse the initial vector: \(-\vec{v}_1\) = 255m/s
  3. Add the vectors: \(-\vec{v}_1 + \vec{v}_2 = 225+160 = 415m/s\)
  4. Positive is east, therefore the change in velocity is 415m/s East

Displacement, Speed and Velocity

• This section will explain the terms and concepts of RECTILINEAR (straight-line), such as position, distance, displacement, speed and velocity.

Center of Mass

• An object’s motion is described in terms of their CENTER OF MASS, a single point which is the balance point of the object.

Position

• Position describes the location of an object at a certain point in time with respect to the origin.
• Position is a vector quantity and therefore requires a direction. The absolute reference frame for the direction is the origin of the object.
• Position is measured in metres.

Distance Travelled

• Distance Travelled describes how far a body travels during a journey.
• Distance is a scalar quantity and is measured in meters.

Displacement

• Displacement is the change in position of an object, and is represented by the symbol \(\vec{s}\)
• Displacement considers only the starting point and ending point
  • In other words, the displacement of an object is the straight-line distance between its start and end points
• Displacement is calculated by subtracting the initial position from the final position
• Displacement is a VECTOR and therefore must have a direction as well as a magnitude

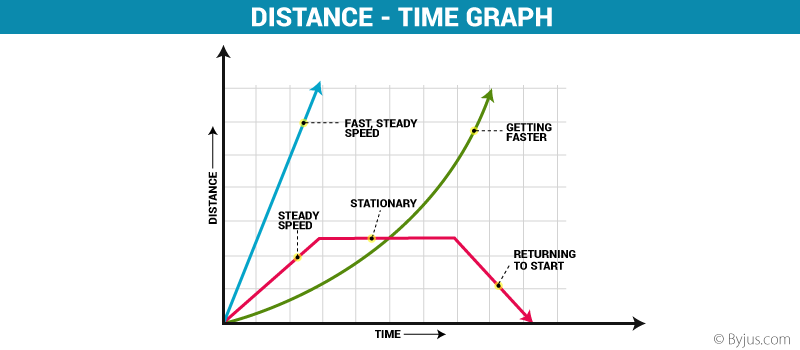
Displacement-Time Graphs

• Displacement-time graphs can be used to summarise the motion of an object
• The gradient of the graph at any point is the velocity at that point

  

Speed and Velocity

• Speed is the rate at which distance is travelled
  • Speed is SCALAR
• Velocity is the rate at which displacement changes
  • Velocity is a VECTOR
• Speed and velocity are both measured in \(m/s^2\)

Instantaneous Speed and Velocity

• How fast an object is moving at a particular point in time
• The instantaneous speed is ALWAYS equal to the magnitude of the instantaneous velocity

Average Speed and Velocity

• Indication of how fast an object is moving over a period of time
• Average Speed: \(v_{av} = \frac{Distance Travelled}{Time Taken} = \frac{d}{\Delta t}\)
• Average Velocity: \(\vec{v_{av}} = \frac{Distance Travelled}{Time Taken} = \frac{\vec{s}}{\Delta t}\)

Converting between km/h and m/s

• To convert km/h to m/s, divide by 3.6
• To convert from m/s to km/h, multiply by 3.6

SUVAT Equations

• These can also be expressed with different subjects: