Table of Contents
ENTHALPY CHANGE
Enthalpy (H) is a measure of the heat content of a system. Absolute enthalpy cannot be measured. However, the change in enthalpy (∆H): the change in the heat content of system during a process, measured at constant pressure.
$ΔH = H_{products} − H_{reactants}$
$H_{products}$ < $H_{reactants}$, therefore ΔH is negative and heat energy released by the system (exothermic).
$H_{products}$ > $H_{reactants}$, therefore ΔH is positive and heat energy absorbed by the system (endothermic).
ENERGY PROFILE DIAGRAMS
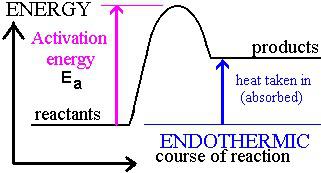
HESS’S LAW OF HEAT SUMMATION
‘The total enthalpy change in a chemical reaction is constant, whether the reaction is performed in one step or several steps.’
Hess’s law is a form of the law of conversation of energy (First law of Thermodynamics).

BOND ENERGIES
Bond energy (or bond enthalpy) is the amount of energy required to break one mole of a bond in a gaseous molecule.
$\Delta H_{rxn} = ∑ ∆H_{\text{reactant bonds broken}} + ∑∆H_{\text{product bonds formed}}$
$∆H_{rxn} = ∑∆H_{\text{reactant bond enthalpy}} − ∑∆H_{\text{product bond enthalpy}}$
ENTROPY
Entropy (S) is a measure of how the available energy is distributed or dispersed amount particles in a system. It is also a measure of energy dispersal (function of temperature). Generally, low entropy → high entropy. (Chaos)
When energy can be distributed in more ways, there is a greater entropy
Entropy is sometimes referred to as the measure of disorder or randomness.
A system with greater possible arrangements (microstates Ω), or greater diversity of movement has higher entropy.
FACTORS THAT CHANGE ENTROPY
Increasing the number of particles → Increases microstates → Increase entropy
Mixing different types of particles → Increases microstates → Increase entropy
Increasing the volume of a container of gas → Increases microstates → Increases entropy o the larger the volume, the more ways there are to distribute the energy
Increasing the number of particles in states with more freedom of movement (gas > liquid > solid)
Molecules becoming more complex → Increases microstates → Increases entropy
Increase temperature → Increases microstates → Increases entropy
SECOND LAW OF THERMODYNAMICS
The second law of thermodynamics states that the entropy of the universe is always increasing.
$ΔS_{universe} = ΔS_{system} + ΔS_{surroundings} \gt 0$
CALCULATING ENTROPY IN CHEMICAL REACTIONS
$ΔS_{rxn} = ∑ ΔS_{products} − ∑ΔS_{reactants}$
GIBBS FREE ENERGY
In any process, the main form of interaction between the system and the surroundings is the exchange of heat.
In an exothermic reaction, heat from the system enters the surrounding and increases temperature, which will increase its entropy. The reverse will be true for an endothermic reaction.
At a lower temperature, the same amount of heat will cause a greater proportional change in entropy.
$ΔS_{universe} = ΔS_{system} + ΔS_{surroundings} \gt 0$
$ΔS_{surroundings }= \frac{−ΔH_{system}}{T}$
$ΔS_{universe} = ΔS_{system} - \frac{−ΔH_{system}}{T} \gt 0$
$−TΔS_{universe} = ΔH_{system} − TΔS_{system} \lt 0$
Josiah Willard Gibbs redefined the quantity −TΔ$S_{universe}$ as free energy or Gibbs Free Energy, 𝚫G.
$Δ𝐺_{system} = ΔH_{system} − TΔS_{system}$
The equation allows the comparison between the relative contributions of the two driving forces for a reaction, entropy and enthalpy.
- If 𝚫G < 𝟎 (Δ$H_{system}$ < TΔ$S_{system}$), a reaction is spontaneous
- If 𝚫G > 𝟎 (Δ$H_{system}$ > TΔ$S_{system}$), a reaction is non-spontaneous
- If 𝚫G = 𝟎, a reaction will occur both in the forward and reverse directions, equilibrium.
| $\Delta H$ | $\Delta S$ | $\Delta G$ | Comments on Reaction |
|---|---|---|---|
| - | + | - | Always Spontaneous |
| + | + | + or - | Spontaneous at high temperatures |
| - | - | + or - | Spontaneous at low temperatures |
| + | - | + | Never spontaneous |
EQUATION SUMMARY
$Q=mc\Delta T$
$ΔH = H_{products} − H_{reactants}$
$∆H_{Combustion}= − \frac{q}{n}$
$∆H_{Solution} = −\frac{q}{n}$
$∆H_{rxn} = ∑∆H_{\text{bond enthalpy of reactants}} − ∑∆H_{\text{bond enthalpy of products}}$
$ΔS_{rxn} = ∑ ΔS_{products} − ∑ΔS_{reactants}$
$Δ𝐺_{system} = ΔH_{system} − TΔS_{system}$
REVERSIBLE REACTIONS
OUTCOMES COVERED
- model static and dynamic equilibrium and analyse the differences between open and closed systems
(ACSCH079, ACSCH091)
investigate the relationship between collision theory and reaction rate in order to analyse chemical equilibrium reactions (ACSCH070, ACSCH094)
explain the overall observations about equilibrium in terms of the collision theory (ACSCH094)
EQUILIBRIUM
For reversible reactions, a reversible arrow is used to indicate that both reactions are capable of proceeding.
$\text{Reactants}\ce{<=>}\text{Products}$
If you know $\LaTeX$, I’d highly recommend right-clicking on the above equation and selecting “Show Math as TeX Commands”. Feel free to laugh at my clunky implementation of getting an equilibrium sign, and understand that this kind of bodging is why we’ve never been first in Google search results 😢
- Pranav
Physical changes are generally reversible.
STATIC AND DYNAMIC EQUILIBRIUM
Reactions will proceed until either a static or dynamic equilibrium is reached. Equilibrium refers to the state of a closed chemical system which:
The concentrations of both reactant and products do not change with time
The rate of the forward reaction is equal to the rate of the reverse reaction
Irreversible reactions (shown with a forward arrow →) that go to completion reach a static equilibrium.
Reversible reactions (shown with a reversible arrow ⇋) do not go to completion. In a closed system, reversible reactions will instead reach a state known as dynamic equilibrium.
At equilibrium, the rates of the forward and reverse reactions are the same, but non-zero.
The equilibrium is dynamic because there are changes occurring at the microscopic level, even though the system undergoes no change at the macroscopic level.
There are no macroscopic changes when a closed system is at equilibrium.
Types of Systems
An open system is a system where matter and energy can enter and leave.
A closed system is a system where matter cannot enter and leave, but energy exchange can take place with the surrounding (in the form of pressure or heat).
An isolated system is a system where neither matter nor energy can leave.
Rates of Reaction
Concentration or Volume/Pressure
Surface Area
Temperature
Presence of catalyst
Reactivity of reactants
COLLISION THEORY
In order for any reaction to proceed, reactants must collide. Particles need to collide with sufficient energy and in the correct orientation for it to be a successful reaction. A collision with sufficient energy and the correct orientation is called an effective collision.
The rate of reaction is how rapidly a reaction proceeds. The rate is defined as the change in the concentration of reactants or products over time. It is dependent on the frequency of effective collisions.
ADDITION/REMOVAL OF A REACTION COMPONENT
If the concentration of one reaction component increases, its rate of reaction will increase as there are more particles to collide with, thus increasing the frequency of effective collisions. The rate of that reaction will be relatively greater than that of the rate of the reverse reaction. This means that more products or reactants will being produced until equilibrium is reached.
Similarly, the reduction in one of the reaction components will reduce its rate of reaction. This occurs as there are fewer particles to collide with which reduces the frequency of effective collisions. The rate of that reaction will be relatively less than the rate of the reverse reaction. This means that more products or reactants will being produced until equilibrium is reached.
CHANGE IN VOLUME OR PRESSURE
A decrease in the volume of a chemical system involving gasses will result in gasses colliding more often. The gas particles will also be colliding with more energy as pressure is inversely proportional to volume. As particles are colliding more frequently and with more energy to overcome the activation energy barrier, the frequency of effective collision increases. Both the rate of the forward and reverse reaction will increase, however, the rate of reaction that uses the greatest number of moles will be relatively greater than the reverse reaction as there are more particles that can collide effectively with each other.
When the volume is increased and pressure is decreased, the partial pressures of all gasses will decrease. Both the rate of the forward and reverse reaction will decrease. The rate of reaction that produces more moles will be relatively greater than the reverse as the reaction is more likely to occur because it requires fewer particles to effectively collide.
Changing the overall pressure of a chemical system does not always cause a disturbance in equilibrium. For example, the addition of inert gasses.
CHANGE IN TEMPERATURE
By increasing the temperature of a chemical system at equilibrium, particles will possess more kinetic energy, which means that more particles (both reactants and products) have enough energy to collide and overcome the activation energy of the forward and reverse reactions.
For an exothermic reaction, the activation energy of the reverse reaction is higher than that of the forward reaction. An increase in temperature means that proportionally more products will be able to collide with enough energy in reverse reaction than the reactants. This causes the rate of the reverse reaction to occur at a faster rate than the forward reaction. Therefore, the concentrations of the reactants will increase whereas the concentration of the products will decrease until a new state of equilibrium is reached.
When the temperature is decreased, all the particles in the system lose energy which decreases both the rate of the forward and the reverse reaction. However, the rate of the reverse endothermic reaction will be relatively higher than the rate of the forward reaction.
OUTCOMES COVERED
- analyse examples of non-equilibrium systems in terms of the effect of entropy and enthalpy.
PHOTOSYNTHESIS
Photosynthesis appears to be the reverse reaction of the combustion of glucose and may seem to be a reversible reaction. However, in nature, the process involves many individual irreversible steps which combine to give the overall reaction; hence photosynthesis is irreversible.
$\color{green}{\ce{6CO2(g) + 6H2O(l) → C6H12O6(s) + 6O2(g)}}$
- $∆H \gt 0$ (endothermic)
- $∆S \gt 0$ (less moles, moving to more order)
- Non-spontaneous at all temperatures
- Chlorophyll is the catalyst for photosynthesis.
- UV rays drive the photosynthesis reaction.
SPONTANEITY AND EQUILIBRIUM
Haber Process
$\color{orange}{\ce{N2(g) + 3H2(g) ⇋ 2NH3(g)}, ∆𝐺 = −33.3 kJmol^{−1}}$
The Gibbs free energy change for this reaction is negative, therefore we would predict that the forward reaction is spontaneous.
The Gibbs free energy change for the reverse reaction will be the negative of this value, $+33.3 kJmol^{−1}$, so we would predict that the reverse reaction is nonspontaneous.
Entropy of mixing allows the reaction to be reversible.
The position with lowest free energy is somewhere in between pure reactants and pure products. This is the position of equilibrium.
The sign of $∆𝐺$ indicates whether reactants or products will dominate the mixture with lowest free energy.
- Since entropy of mixing always exist, technically no reaction is strictly irreversible. However, if the position of equilibrium lies very close to the products, the reaction is called “irreversible” as the reverse reaction will not occur to any observable extent.
This is when Gibbs free energy is very negative.
- Reversibility of a reaction can also be considered in terms of activation energy. Reactions are unlikely to be reversible as molecules will not have sufficient energy.
in order for a reaction to be reversible, the forward and reverse reaction must have a small activation energy.
LE CHATELIER’S PRINCIPLE
OUTCOMES COVERED
investigate the effects of temperature, concentration, volume and/or pressure on a system at equilibrium and explain how Le Chatelier’s principle can be used to predict such effects, for example:
heating cobalt(II) chloride hydrate
interaction between nitrogen dioxide and dinitrogen tetroxide
iron(III) thiocyanate and varying concentration of ions (ACSCH095)
examine how activation energy and heat of reaction affect the position of equilibrium
RATES OF REACTION (FROM MODULE 3)
The rate of reaction is the speed with which reactants are converted to products, or how rapidly a reaction proceeds.
Rate is defined as the change in concentration of reactants or products over time. - The rate of reaction depends on the frequency of effective collisions.
$\color{orange}{\text{Rate of Reaction} \propto \text{Frequency of Effective Collisions}}$
FACTORS AFFECTING THE RATE OF REACTION
Nature of reactants
Concentration
Surface area
Temperature
Catalysts
Pressure/Volume
Nature of Reactants
Every reaction has its own rate and its own activation energy, depending on the reactivity of the reactants.
Aqueous solutions already have dissociated ions. They do not need to collide in any correct orientation and usually have very low $E_a$.
Concentration
The rate of reaction increases when the concentration of reactants is increased.
- The rate of reaction is directly proportional to the reactant concentration.
- Increasing the concentration increases the number of effective collisions.
- Increases the number of particles in a given space.
Particle Size/Surface Area
The rate of reaction increases when the surface area of reactants is increased.
- Exposes more particles to the reactant. This increases the chance of a successful collision which therefore increases the rate of reaction.
Temperature
The rate of reaction increases when the temperature of the reactants is increased.
- The total number of collisions increase. o Increased KE, particles move faster. There is a greater chance of successful collision.
When the temperature increases, the average kinetic energy of the molecules increase, thus molecules move faster which means they collide more frequently.
The average energy of the collisions increases. Therefore, a higher fraction of collisions exceeds activation energy.
In general, reaction rate doubles every 10 degrees Celsius.

Catalysts
A catalyst is a substance that increases the rate of reaction without being consumed.
Catalysts work by allowing the reaction to take an alternative reaction pathway with a lower activation energy.
LE CHATELIER’S PRINCIPLE
In 1888, a French chemist called Henri Le Chatelier (1850-1936) put forth the statement known as Le Chatelier’s Principle:
“If a system at dynamic equilibrium is disturbed by changing the conditions, the system undergoes a reaction which minimises the effect of the disturbance to attain a new equilibrium”
A chemical system at equilibrium can be disturbed in the following ways:
Change in concentration
Change in pressure → Change in volume →Change in concentration - Change in temperature
Le Chatelier’s principle is a convenient method for predicting equilibrium shifts, but does not explain why it shifts. Collision theory explains the shift in equilibrium.
THE HABER PROCESS
CHANGE IN CONCENTRATION
$\ce{N2(g) + 3H2(g) ⇋ 2NH3(g)}, ∆H = −92kJ mol^{−1}$
Adding A Reaction Component
Addition of $\ce{H2(g)}$ increases $\ce{H2(g)}$. This will result in the rate of the forward reaction to increase, meaning the forward reaction has been favoured.
Since the rate of the forward reaction is different to the rate of the reverse reaction, the equilibrium has been disturbed.
Generally, the reaction that counteracts the disturbance will be favoured; in other words, its rate will increase relative to the other reaction.
Removing a Reaction Component
Removing $\ce{N2(g)}$ decreases $\ce{N2(g)}$. This will result in the rate of the reverse reaction to increase, meaning the reverse reaction has been favoured.
The reaction that counteracts the disturbance will be favoured; in other words, its rate will increase relative to the other reaction.
CHANGE IN VOLUME (OR PRESSURE)
The pressure exerted by a gas arises from the force of the gas particles colliding with the walls of the container.
Therefore, the pressure is proportional to the number of gas particles present.
$\text{Pressure }\propto\text{ Moles of gas}$
Boyle’s Law states that pressure and volume are inversely proportional to each other.
$$Pressure \propto \frac{1}{Volume}$$
Doubling the volume of the container decreases pressure. To counteract this effect, the reaction will shift in the direction that produces the most amount of moles. Therefore, the reverse reaction will be favoured.
Doubling the pressure of the container decreases volume. To counteract this effect, the reaction will shift in the direction that produces the least amount of moles. Therefore, the forward reaction will be favoured.
CHANGE IN TEMPERATURE
The effect of a change in temperature on a reaction at equilibrium depends on whether the forward reaction is exothermic or endothermic.
$\ce{N2(g) + 3H2(g) <=> 2NH3(g)}, ∆H = −92kJ mol^{−1}$
If temperature of the system is increased, the reverse reaction will be favoured to counteract this effect. The reverse reaction is endothermic and will be favoured.
ADDITION OF A CATALYST
A catalyst increases the rate of a chemical reaction without being consumed, by providing an alternate pathway of lower activation energy. The addition of a catalyst reduces the activation energy of both the forward and reverse reaction by the same amount.
Therefore, the addition of a catalyst will not disturb the equilibrium
The concentrations of the components are not affected, by the system will reach equilibrium faster
ADDITION OF INERT GAS
The addition of an inert gas will increase pressure, but equilibrium will not be disturbed. This is because the concentrations of reactants and products remain the same, if the volume of the container does not change.
DIMERISATION OF NITROGEN DIOXIDE
$\ce{2NO2(g)<=>N2O4(g)}, \Delta=-58kJmol^{-1}$
When colourless dinitrogen tetroxide gas $(\ce{N2O4})$ is enclosed in a vessel, a brown colour will appear indicating the formation of nitrogen dioxide $(\ce{NO2}).$
The intensity of the brown colour indicates the amount of nitrogen dioxide present in the vessel.
The dimerization of nitrogen dioxide is an exothermic process
Summary
A shift in the forward direction is called a shift towards the right side.
A shift in the reverse direction is called a shift towards the left side.
Equilibrium will shift to remove an added component (away from component)
Equilibrium will shift to replace a removed component (towards the component)
An increase in volume will cause equilibrium to shift towards the side with more gas moles. - A decrease in volume will cause equilibrium to shift towards the side with fewer gas moles.
ANSWERING LE CHATELIER’S PRINCIPAL QUESTIONS
Clearly explain the effect of changes in conditions on the yield of equilibrium reactions.
State that the change in reaction conditions disturbs the equilibrium.
“According to Le Chatelier’s principle, the position of equilibrium shifts left/right”
Justify the shift:
a. “To replace/remove”
b. “To the side with more/less gas moles, to increase/reduce pressure”
c. “In the exothermic/endothermic direction, to replace/remove heat”
…and minimise the disturbance
State the effect of the shift, “Therefore, the concentrations of the reactants/products increase/decrease.”
QUALITATIVE ANALYSIS OF EQUILIBRIUM
OUTCOMES
investigate the effects of temperature, concentration, volume and/or pressure on a system at equilibrium and explain how Le Chatelier’s principle can be used to predict such effects, for example:
heating cobalt(II) chloride hydrate
interaction between nitrogen dioxide and dinitrogen tetroxide
iron(III) thiocyanate and varying concentration of ions (ACSCH095)
CONCENTRATION PROFILE DIAGRAMS
The changes occurring in a system can be identified by examining the shape of the line in a concentration profile diagram during a particular time period.
- The x-axis is time or reaction progress
- The y-axis is concentration or partial pressure
| Graph Feature | Disturbance |
|---|---|
| Concentration of one component spikes up, then all concentrations change | Increase [concentration] of a component |
| Concentration of one component spikes down, then all concentrations change | Decrease [concentration] of a component |
| Concentrations of all components spike up, then all concentrations change | Decrease volume → Increase pressure → Increase [concentrations] of components |
| Concentrations of all components spike down, then all concentrations change | Increase volume → Decrease pressure → Decrease [concentrations] of components |
| There are no spikes in the graph, then all concentrations change | Change in temperature |
| Concentrations are flat | Nothing (system at equilibrium) |
EQUILIBRIUM CONSTANT
- deduce the equilibrium expression (in terms of $K_{eq}$) for homogeneous reactions occurring in solution (ACSCH079, ACSCH096)
explore the use of $K_{eq}$ for different types of chemical reactions, including but not limited to: – dissociation of ionic solutions
EQUILIBRIUM CONSTANT EXPRESSION
A quantitative way of describing the position of equilibrium is the equilibrium constant $(𝐾_{𝑒𝑞}).$
$\ce{aA + bB <=> cC +dD}$
Capital letters represent chemical substances
Lower case letters represent the stoichiometric coefficients of the balanced equation
$K_{eq}=\frac{[C]^{c}\cdot [D]^{d}}{[A]^{a}\cdot [B]^{b}}$
In an ideal system, the value of K is constant at constant temperature.
PURE, LIQUIDS AND SOLIDS
In heterogeneous systems, some of the components are in different phases:
$\ce{CaCO3_{(s)}<=>CaO_{(s)} +CO2_{(g)}}$
The concentrations of pure solids and pure liquids cannot change at a constant temperature.
- Because the equilibrium constant is only concerned with concentrations that change as they approach equilibrium, eliminate the terms for pure solids or liquids.
- The concentrations disappear from the equilibrium constant expression.
- Only gases and aqueous species appear in the equilibrium, except if all the reactant and products are all liquids.
INTERPRETING THE EQUILIBRIUM CONSTANT
The larger the value of K, the further the equilibrium lies towards the RHS. A reaction with a very large K, proceeds almost to completion.
The smaller the value of K, the further the equilibrium lies towards the LHS. A reaction with a very small K, proceeds barely at all.
K AND THE DIRECTION OF REACTION
If concentrations are substituted into the expression at any point, the value is called Q, the reaction quotient.
$Q=\frac{[C]^{c}\cdot [D]^{d}}{[A]^{a}\cdot [B]^{b}}$
The relative values of Q and K determines which way the reaction will proceed to reach equilibrium.
If $𝑄 = 𝐾,$ then the system is at equilibrium
If $𝑄 \gt 𝐾,$ then the backwards reaction will be favoured
CALCULATIONS WITH QUADRATIC EQUATIONS
In some calculations, it will be required to solve a quadratic equation to determine $x$.
In these calculations, simplification can be used to make the calculation less complicated to solve:
- If K is very small, then $x$ will be very small, and the calculation can be simplified by using the following approximation:
$[Reactant]{initial} − x \approx [Reactant]{initial}$
- However, the assumption must be checked to be valid. The calculated value of $x$ must be less than 5% of the reactant’s initial concentration. If the assumption is invalid, the quadratic formula has to be used.
EFFECT OF TEMPERATURE ON $𝑲_{𝒆𝒒}$
When temperature is increased, equilibrium shifts so that the endothermic reaction is favoured, whether it is the forward or the reverse reaction. Therefore, unlike changes in concentration and pressure, a change in temperature is the only factor that will change the value of K.
For exothermic reactions, K increases with lower temperatures and decreases with higher temperatures.
For endothermic reactions, K decreases with lower temperatures and increases with higher temperatures.
IRON(III) THIOCYANATE
conduct an investigation to determine $K_{eq}$ of a chemical equilibrium system, for example:
$K_{eq}$ of the iron(III) thiocyanate equilibrium (ACSCH096)
IRON (III) THIOCYANATE EQUILIBRIUM REACTION
When mixed together, aqueous solutions of iron(III) nitrate $\ce{(Fe(NO3)3)}$and potassium thiocyanate $\ce{(KSCN)}$ combine, in a reversible exothermic process, to form the aqueous iron(III) thiocyanate complex $(\ce{\ce{Fe(SCN)^2+}(aq)}).$
$\ce{Fe^3+{(aq)} + SCN-{(aq)} <=> Fe(SCN)^2+_{(aq)}}$
Iron(III) ions are very pale yellow colour, while iron(III) thiocyanate complex is an intense deep red colour. When diluted and at equilibrium, the colour of the mixture containing all three species is amber.
EQUILIBRIUM SHIFTS
A shift to the RHS, increase concentration of $\ce{Fe(SCN)^2+}$ → More intense
Cool down system: ice water bath
Increase $\ce{Fe^3+}$ and $\ce{SCN-}$: Add more $\ce{FeCl3}$ and $\ce{KSCN}$
A shift to the LHS, decreases concentration of $\ce{Fe(SCN)^2+}$ → Less intense
Heat system: Hot water bath (Approx. 70 degrees Celsius)
Decrease $\ce{Fe^3+}$ and $\ce{SCN-}$: Add $\ce{NaOH}$ and $\ce{AgNO3}$
Summary
Since thiocyanate ions bind to iron via the nitrogen atom, the formula of the iron(III) thiocyanate complex is sometimes written as $\ce{\ce{Fe(SCN)^2+}}$.
SPECTROPHOTOMETRY
Spectrophotometry is an analytical technique that is used to determine the concentration of a substance in a solution.

Iron(III) thiocyanate strongly absorbs light at a wavelength of 447 nm and reflects light that is mostly orange-red, hence we see it as orange-red in colour.
Iron(III) thiocyanate absorbs light blue light.
When it absorbs the light, electrons are transitioning from lower to higher quantised energy levels. The energy gap between the levels is equal to the energy of the 447 nm wavelength light.
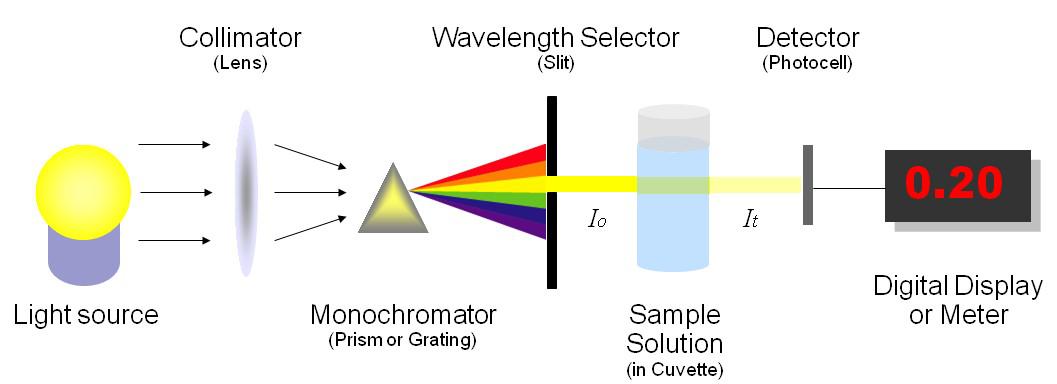
A UV/Vis spectrophotometer like the one shown measure the intensity of light passing through a sample solution in a cuvette.
A lamp provides white light (continuous source, which is narrowed and aligned into a beam using a slit.
A prism splits the light into different wavelengths and is rotated so the desired wavelength of light passes through the monochromator (exit slit).
The light beam passes through the sample, which absorbs a fraction of the light. The greater the concentration of iron(III) thiocyanate, the greater the absorption of 447 nm light.
The remaining light is transmitted through the sample and reaches a detector, which converts the amount of light to an electrical signal.
A spectrophotometer expresses the intensity of light in absorbance (A).
$A=log_{10}\frac{I_{0}}{I}$
- A: Absorbance, a number typically between 0.3 - 2.5. It is dimensionless but often expressed in absorbance units (AU)
- $I_{0}$: The intensity of light passing through the blank (reference) sample.
- I: The intensity of light passing through the analyte sample.
Absorbance is proportional to both concentration and the length of the sample, according to the Beer-Lambert Law.
$A=\epsilon lc$
ε: Extinction coefficient (also known as molar absorptivity), a constant that relates absorbance with concentration and path length, with the units $L/cm/mol$
l: Path length of sample in $cm$
c: Concentration of the substance in the sample in $mol/L$
SOLUBILITY
- describe and analyse the processes involved in the dissolution of ionic compounds in water
PROPERTIES OF IONIC COMPOUNDS
A process where equilibrium is often established is in the dissolution of ionic compounds in water.
Ionic compounds contain both cations and anions.
They have an electrostatic attraction between oppositely charged ions.
They are:
- Brittle
High MP, BP
- Solids at room temperature
- Molten and aqueous state conducts electricity
SOLUTIONS OF IONIC COMPOUINDS
Soluble ionic compounds will dissolve in water to form aqueous solutions. When a soluble ionic compound is added to water, the ions at the surface of the crystal become surrounded by water molecules.
Some molecules of water separate from one another and are able to pack closer to the cations and anions of the ionic salt. o They form ion-dipole forces between the molecules.
Solute: Ionic salt
Solvent: Water
When the ion-dipole forces between the ions and the permanent dipoles of the water molecules (adhesive forces) become stronger than the ionic bonds between the ions and the hydrogen bonding within the water (cohesive forces), the ions are dislodged from their position in the crystal.
- The ionic compound dissociates into its component ions. - The ions become solvated.
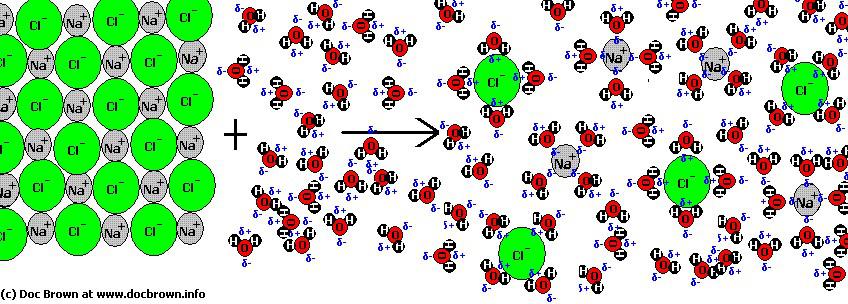
The solvated or hydrated ions are surrounded by a shell of water molecules known as a solvation layer.
- The solvation layer acts as a cushion and prevents a solvated anion from colliding directly with a solvated cation, and therefore keeps the ions in the solution.
Many ionic compounds are soluble in water and will dissociate to form aqueous solutions.
However not all ionic compounds are soluble in water. For example, $\ce{AgCl}$ and $\ce{Ca3(PO4)2}$ are insoluble.
The insolubility of these ionic compounds is due to their strong ionic bonds which cannot be disrupted by the adhesive ion-dipole forces between solute ions and water molecules. Hence the ions do not become dislodged from their positions in the crystal.
Entropy can also contribute to solubility. Most dissolutions are entropically favourable $(∆S \gt 0)$, but some dissolutions are unfavourable.
- The solution consists of the solute and the solvent, so the change in entropy of each part can be considered separately to determine the overall change in entropy for the dissolution process:
$∆S_{Solute} + ∆S_{solvent} = \sum{∆S}$
Depending on the relative magnitude of the effects, total entropy can increase or decrease for the overall system when dissolution occurs, although in majority of cases overall entropy will increase.
An overall decrease in entropy sometimes occurs for ions with high charge density as they interact strongly with water molecules, so the water molecules are held tightly around the solvated ions.
INCREASE IN ENTROPY
Solute in a solid state has a fixed ordered arrangement. Dissolved solute has free mobile ions. Therefore, there is an increase in entropy as the number of possible arrangements increases.
DECREASE IN ENTROPY
Pure water molecules are in random arrangements and are also mobile. When water becomes a solvent, molecules solvate the solute and has less possible arrangements decreasing entropy.
Summary
“Clear” means that light can pass through the substance without being scattered.
“Colourless” means the substance is not coloured. Solutions are clear, but not necessarily colourless."
OUTCOMES
- conduct an investigation to determine solubility rules, and predict and analyse the composition of substances when two ionic solutions are mixed, for example:
potassium chloride and silver nitrate
potassium iodide and lead nitrate
sodium sulphate and barium nitrate (ACSCH065)
PRECIPITATION
The production of an insoluble compound, usually by reacting two soluble compounds.
$\ce{NaCl(aq) + AgNO3(aq) → AgCl(s) + NaNO3(aq)}$
When two clear solutions are mixed together, an insoluble compound is formed. This is called a precipitate reaction. Precipitation reactions are used to remove minerals from drinking water, to remove heavy metals from wastewater and in purification plants of reservoirs.
Solubility Rules
| Ion | Soluble? | Exceptions |
|---|---|---|
| $NO_{3}^-$ | ✅ | ❌ |
| $ClO_{4}^-$ | ✅ | ❌ |
| $Cl^-$ | ✅ | $Ag, Hg_2 , Pb$ |
| $I^-$ | ✅ | $Ag, Hg_2 ,Pb$ |
| $SO_{4}^{2-}$ | ✅ | $Ca, Ba, Sr, Hg, Pb, Ag$ |
| $CO_{3}^{2-}$ | ❌ | Alkalis and Ammonium |
| $PO_4 ^{3-}$ | ❌ | Alkalis and Ammonium |
| $OH^-$ | ❌ | Alkalis, $Ca, Ba, Sr$ |
| $S^{2-}$ | ❌ | Alkalis, Alkaline Earths, Ammonium |
| $Na^+$ | ✅ | ❌ |
| $NH_4 ^+$ | ✅ | ❌ |
| $K^+$ | ✅ | ❌ |
SOLUBILITY
The solubility of a compound is the maximum amount of solute that can dissolve in a specific volume of solvent at a certain temperature.
EQUILIBRIA IN SATURATED SOLUTIONS
When a solvent has dissolved all the solute it can at a given temperature, the resulting solution is saturated.
Any solution containing less solute than this is unsaturated.
If more solute is added to a saturated solution, no more will dissolve.
In a saturated solution, the system is in dynamic equilibrium:
All of the species – the ionic solid and dissolved ions – are present in the final mixture.
The forward reaction is occurring at the same rate as the reverse reaction. In other words, when an ion dissolves, another ion is precipitating at the same time.
The equilibrium constant for these solution equilibria is called the solubility product constant $(𝐾_{𝑠𝑝})$.
- The equilibrium constant is for the equation written in the direction of the dissolution.
UNITS OF CONCENTRATION
MOLARITY
Molarity is the main unit of concentration used in chemistry:
$molarity (c) =\frac{\text{moles of solute (n))}}{\text{Volume of solution (V)}}$
- The volume of solution is expressed in litres (L).
the volume of the total solution (solute + solvent) is used calculate concentration.
PERCENTAGE BY MASS OR WEIGHT (% M/M OR % W/W)
Percentages by mass and weight are both extensively used in industry.
% m/m is an abbreviation for the percentage mass of a substance relative to the total mass. This is the same as percentage weight (% w/w).
- Percentage is given by the formula:
$$\text{% by mass} =\frac{\text{Mass of Solute} \times 100}{\text{Mass of Solution}}$$
- % w/w or m/m can be interpreted as grams of solute per 100g.
- Note: the formula requires the total mass of the solution, not solvent.
PERCENTAGE BY VOLUME (% V/V)
Percentages by mass and weight are both extensively used in industry.
The Percentage by volume is given by the formula:
$$\text{% of volume}=\frac{\text{volume of solute}}{\text{volume of solution}}\times 100$$
MASS PER VOLUME (M/V)
Mass per volume is used in pharmacy and medicine.
Mass per volume is used to measure the blood alcohol level of drivers.
A blood alcohol level of 0.01 refers to 0.010g / 100mL of blood
PARTS PER MILLION & PARTS PER BILLION
- Parts per million and parts per billion (ppm and ppb) are useful when describing very dilute solutions.
$$\text{concentration (ppm)}=\frac{\text{mass of solute (mg)}}{\text{mass of solution (kg)}}$$
$$\text{concentration (ppb)}=\frac{\text{mass of solute }(\mu g)}{\text{mass of solution }(kg)}$$
Many native foods eaten by Aboriginal and Torres Strait Islander people are poisonous and need to be detoxified before consumption
There are several physical and chemical processes user for detoxification:
COOKING OR ROASTING (CHEMICAL REACTION)
The food items are heated in an oven or fire
The heat causes the toxins to decompose
LEACHING (PHYSICAL CHANGE)
The food items are cut up into smaller pieces and soaked in running water.
Water-soluble toxins are washed away.
FERMENTATION OR PROLONGED STORAGE (CHEMICAL REACTION)
- The food items are stored for long periods (several months to several years)
- During this time, various biological processes occur that break down the toxins.
- They are digested by fungi, or broken down by the plant's natural enzymes. (Biological catalysts)
CYCADS (MACROZAMIA)
Cycads are palm-like plants that produce seeds in cones. Cycad seeds are a rich source of carbohydrates and have been eaten in regions of Northern Australia for thousands of years. However, the seeds contain highly toxic chemicals.
The two main types are cycasin and b-methylamino-l-alanine (BMAA).
To prepare them, Aboriginal and Torres Strait Islander people who ate these seeds would commonly prepare them by:
Cooking the seeds in an oven or fire
Cutting the seeds open and leach them in running water for around a week
Fermentation or storage for several months, or several years (some groups stored them for more than three years)
THE POISON, CYCASIN
Cycasin $(\ce{C8H16N2O7})$
Methylazoxmethanol glucoside
Molar Mass = 252.22g/mol
pKa = 12.21 (measure of acidity)
Solubility
56.6 g/L @ 25 degrees Celsius in water/diluted ethanol
Sparingly soluble in absolute ethanol
Insoluble in benzene, chloroform + acetone
Decomposition
Melting point @ 144 degrees Celsius
Decomposes at 154 degrees Celsius
Produces $\ce{N2}$
MORETON BAY CHESTNUT (BLACK BEAN)
The Moreton Bay Chestnut is found on the east coast of Australia. It produces pods containing large seeds that are toxic. Eating unprocessed seeds causes vomiting and diarrhoea. When cooked, processed seeds taste like sweet chestnuts.
SOLUBILITY CALCULATIONS
CALCULATING $𝑲_{𝒔𝒑}$ FROM SOLUBILITY
An equilibrium is only present in a saturated solution where the maximum amount of ionic compound has dissolved. Therefore, the solubility of a substance, whether given in moles per litre or mass per volume, can be used to calculate the solubility constant $K_{sp}.$
PREDICTING THE FORMATION OF A PRECIPITATE
Solubility constants can be used to predict if a precipitate will form when two solutions are mixed.
$\ce{Ba(OH)2(𝑠) ⇋ Ba+(𝑎𝑞) + 2OH− (𝑎𝑞)}$
$𝐾_{s𝑝} = \ce{[Ba^{2+}][OH^{2-}]}$
The solubility constant for this reaction at 25℃ is 2.55 × 10^−4^
This means $\ce{[Ba^{2+}][OH^{2-}]}= 2.55 × 10^{−4}$ in a saturated solution.
If the concentration of $Ba^{2+}$ and $OH^{-}$ are higher than the amounts in a saturated solution, 𝑄 > $𝐾_{𝑠𝑝}$ and precipitation will occur.
If the concentration of $Ba^{2+}$ and $OH^{-}$ are lower than the amounts in a saturated solution, 𝑄 > $𝐾_{𝑠𝑝}$ and precipitation will not occur.
THE COMMON ION EFFECT
In an aqueous solution of an ionic compound, the ions are dissociated.
This means that the ions separate into individual solvated ions.
Ions of the same species are indistinguishable, regardless of where they originated.
This means that in a saturated solution, if another substance is added that has an ion in common with the first substance, it will affect the position of equilibrium, leading to lower solubility. This is known as the common ion effect.
SOLUBILITY CURVES (SOLUBILITY AND TEMPERATURE)
Since dissolution is a reversible process, the position of equilibrium (extent of dissolution) will depend on temperature.
The relationship between solubility and temperature can be seen on a solubility curve, which shows the maximum amount of solute that can dissolve at a range of temperatures.
DISSOCIATION OF ACIDS
ACID STRENGTH
Acids differ in their strength: the extent of ionisation or dissociation in water.
- A stronger acid will ionise further
Strong acids completely dissociate in water
- Straight arrows are used to indicate that these dissociations are irreversible and proceed to completion.
Weak acids partially dissociate in water.
- Reversible arrows are used indicate that these dissociations proceed to equilibrium.
The acid dissociation constant is the equilibrium constant for the dissociation (ionisation) of an acid into hydrogen ions $(H^+)$ and an anion $(K_a)$.
Acids that can produce more than one $H^+$ ion are known as polyprotic acids.
- The dissociation of each $H^+$ ion occurs stepwise, and an acid dissociation constant is assigned to each step.
$$\begin{gather*}\bbox[5px, border: 2px solid orange]{\ce{H3PO4<=>H+ +H2PO4-}} \\ \bbox[5px, border: 2px solid orange]{K_{a1}=\frac{\ce{[H+][H2PO4-]}}{\ce{[H3PO4]}}=7.52\times10^{-3}} \\ \bbox[5px, border: 2px solid green]{\ce{H2PO4- <=> H+ +HPO4^2-}} \\ \bbox[5px, border: 2px solid green]{K_{a2} =\frac{\ce{[H+][HPO4^2-]}}{\ce{[H2PO4-]}}=6.23\times10^{-8}} \\ \bbox[5px, border: 2px solid pink]{\ce{HPO4^2- <=>H+ +PO4^3-}} \\ \bbox[5px, border: 2px solid pink]{K_{a3}=\frac{\ce{[H+][PO4^3-]}}{\ce{[HPO4^2-]}}=2.20\times10^{-13}} \end{gather*}$$
Acid strength depends on the identity of the acid and the extent of its ionisation in water.
PH SCALE
The acidity of a solution is determined by both the strength and the concentration of the acids present.
The concentration of the hydrogen ions in a solution are generally small. The pH scale, a logarithmic scale, is a convenient way of expressing [$\ce{H+}$] as a number generally between 0 (extremely acidic) and 14 (extremely basic).
A pH of 7 represents a neutral solution. The further away from 7, the more acidic or alkaline the solution.
pH can be calculated from the [$\ce{H+}$] using the equation:
$𝑝H = −[H^+]$
𝑝 stands for $−𝑙𝑜𝑔_10$, and the concentration of the hydrogen ions are in $mol/L$
The notation $pH$ derives from the French pouvoir hydrogene, meaning the “power of hydrogen”
DEGREE OF IONISATION
To calculate the percentage of any component in a sample, the formula is:
$$\text{% Ionisation}=\frac{component}{total}\times 100\text{%}$$
For a weak acid, $\ce{HA}$:
$HA_{(aq)}\ce{<=>H+(aq) +A-(aq)}$
The percentage ionised (degree of ionisation):
$% ionised=\frac{[H^+]{eqm}}{[HA]{initial}}\times 100=\frac{[H^{-}]{eqm}}{[HA]{initial}}\times 100$
The percentage unionised (percentage of intact molecules):
$% unionised=\frac{[HA]{eqm}}{[HA]{initial}}\times 100=100-%ionised$

